Binary Numbers
COUNTING SYSTEMS UNLIMITED . . . Since you have been using
the
10 different digits 0, 1, 2, 3, 4,
5, 6, 7, 8, and 9 all your life, you may wonder how it is possible to count and
do arithmetic without using all 10. Actually, there is no advantage in using 10
counting digits rather than, say,
8, 12, or 16. The 10-digit system
(called the decimal system, since the word "decimal" means
"based on 10") probably came into universal use because man first
started to count by using his fingers, and there happen to be 10 of them.
To see how to count by using other than 10 digits, notice
how we count in the ordinary decimal system. We represent a number higher than
9, the highest digit, by a combination of two or more digits. The number next
after 9 is 10, and then 11, etc. After we reach 99, the highest number that can
be written with two digits, we start using three digits. The number next after
99 is 100, and then comes 101, etc.
Now let's try counting in the octal
system. "Octal" means "based on eight"; that is,
we use only the eight digits 0, 1, 2, 3, 4, 5, 6, and 7. The digits 8 and 9 are
not used. So now what do we do after we have counted to 7? Since we have used
up all the symbols we are permitted to use, we write 10 as the next number and
then comes 11 and so on up to 17. After
17 comes 20.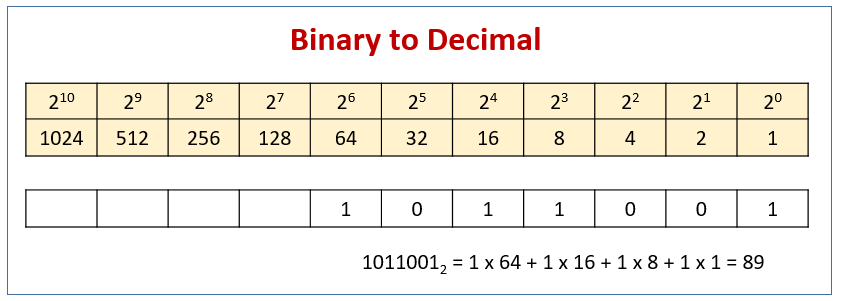
Related Articles
Lesson meta keywords and meta description:
Write a public review